1.3 Forming a Falsifiable Hypothesis

Topic Summary

Once you’ve posed a worthwhile question, the next step is to make a guess about what the answer might be. Such a guess is often called a hypothesis. A hypothesis is a tentative guess – hopefully an educated one – about the explanation behind something. It leads to a prediction about what you might find when you look into data.

People often skip this step, but it can be helpful to at least jot down the answer you think you’ll get from your data. Forming a hypothesis doesn’t have to be complicated, and it doesn’t have to take more than a minute or so – sometimes even less than that. But it’s critical that your hypothesis be falsifiable, that is, written in such a way that it’s at least theoretically possible to prove it wrong.

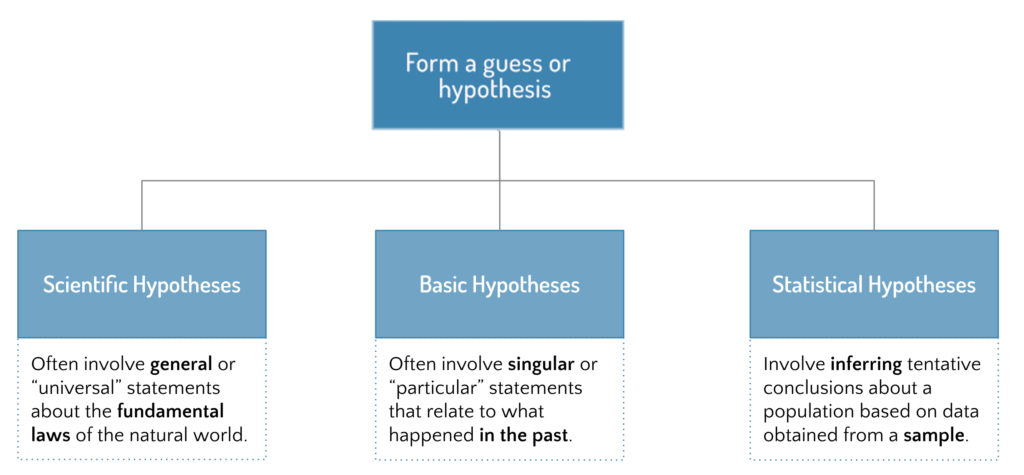
In this topic, we’ll consider how to form a hypothesis, and we’ll cover three different categories of hypotheses that you can use on your journey from data to wisdom: a scientific hypothesis, a basic hypothesis, and a statistical hypothesis. We’ll also consider two different forms of reasoning – induction and deduction – and how to avoid a common pitfall called the “inductive fallacy.”

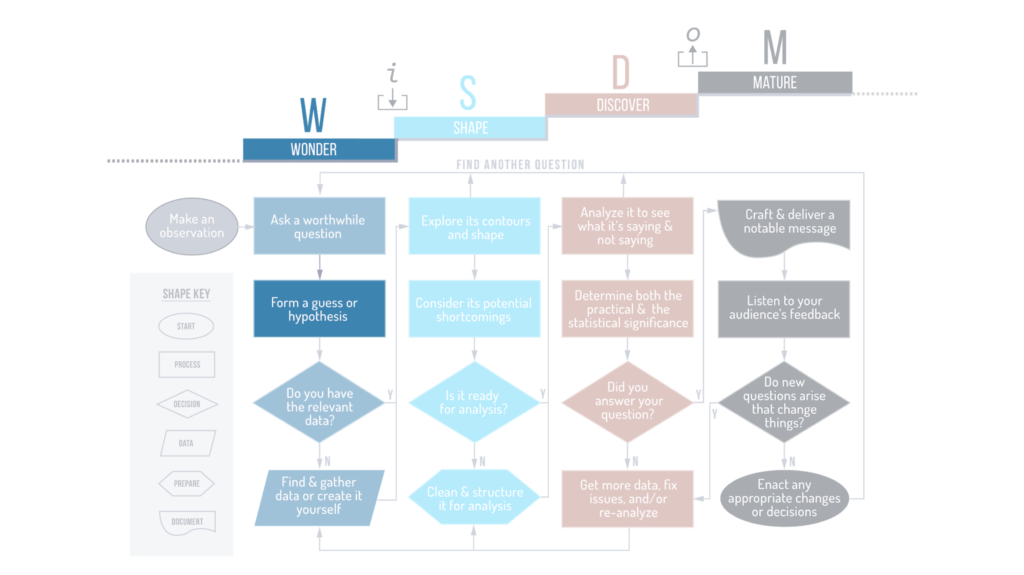
Where are You in the Flowchart?

The WISDOM Data-Working Flow, with the third step of the first phase highlighted: WONDER - Form a falsifiable hypothesis.

Key Points To Remember

  • There are three kinds of hypotheses we consider in this lesson:
    • A scientific hypothesis is most often a universal statement, also called a general statement, about the way things work in the natural world, and is connected to an experiment in which you predict the outcome based on a theory you have about some general law of the universe.
    • A basic hypothesis, on the other hand, is often nothing more than a particular statement, also called a singular statement, about the answer to a question about something that’s very specific. “How did sales of Product A change over the last two quarters? My guess is that sales increased by 25%.”
    • A statistical hypothesis comes into play whenever you’re dealing with sample data (like a survey) rather than population data, and you want to form tentative conclusions about the many based on data collected from the few. One way to do so is called Null Hypothesis Statistical Testing (NHST) and it involves two hypotheses: a null hypothesis and an alternative hypothesis.
      • The null hypothesis (H0) states that any difference you notice in the data is due to chance alone.
      • The alternative hypothesis (Ha or H1) states the opposite – that any difference you see is not due to chance alone, but rather due to some actual difference in the groups you’re testing.
  • Any good hypothesis needs to be falsifiable, that is, at least theoretically possible to prove it wrong if it is in fact wrong. Some statements, such as “it will rain in Seattle tomorrow,” are possible to prove wrong. You just wait until tomorrow, and then observe whether it rains in Seattle or not. However, other statements, such as “it will either rain or not rain in Seattle tomorrow” simply can’t be proven wrong; they’re not falsifiable.
  • There are two forms of reasoning:
    • induction – reasoning from specific observations to general rules. You notice something is true once, twice, a third time, and eventually you start thinking that it might be always true.
    • deduction – reasoning from general rules to specific observations. You believe that a general rule exists that something is always true, so you reason that it must be true in a specific instance.
  • It’s important to understand these concepts so that you can avoid the inductive fallacy, in which you make a faulty generalization from observations of specific instances (“that swan is white”) to a general rule about the way things are (“all swans are white”). To avoid this mistake, you need to keep in mind that induction is useful for forming hypotheses to test, but it’s not a logically valid way to form broad and sweeping conclusions. Just because your data shows you a fact that was true in a specific situation doesn’t mean that fact will always be true in every situation.
    • No amount of singular statements (observations) that confirm a general statement (such as a universal scientific theory) can conclusively prove it to be true, or verify it. However, it only takes one singular statement that refutes a general statement to prove it to be false, that is, to falsify it.

Definitions

  • falsifiability – A hypothesis is said to be falsifiable if it takes the form of a statement that’s at least theoretically possible to prove wrong.
  • singular or particular statement – Attributes some property to a particular individual or object (e.g., “Socrates was wise”).
  • general or universal statement – Isn’t about any particular individual or object. It refers to indefinitely many facts (e.g., “All philosophers are wise”).
  • population – The set of all members that share at least one trait in common. If you have data from an entire population, you can find a parameter, such as average height of all people in the population.
  • sample – A smaller number of members taken from an overall population. If you only have data from a sample, you can only find a statistic, such as the sample mean of heights of the people included in the sample.

Diagrams

Flow chart with form a guess or hypothesis at the top, branched out into three branches: Scientific Hypotheses, Basic Hypotheses, and Statistical Hypotheses. Scientific Hypotheses often involve general or “universal” statements about the fundamentals laws of the natural world. Basic Hypotheses often involve singular or “particular” statements that relate to what happened in the past. Statistical Hypotheses involve inferring tentative conclusions about a population used on data obtained from a sample.
Flow chart for the third step of the WONDER phase: Forming a falsifiable hypothesis. It begins with defining a question, then doing background research, then forming a hypothesis and prediction, then designing and conducting an experiment, then analyzing the data, and finally, to drawing conclusions. This either leads you to publishing the results or back to the second step in the flow chart, doing more background research.
Flow chart for the two forms of reasoning - Induction and Deduction. Induction involves deriving hypotheses and deduction involves testing hypotheses. General statements are made based on laws and theories, which leads to testing hypotheses (deduction), which leads to singular statements based on observations and empirical evidence, which leads to deriving hypotheses (induction), which leads back to general statements.

Course Project

Think about the question you have posed and form a hypothesis about the answer to that question.

  • A basic hypothesis – use this form of hypothesis if your question relates to historical data and you’ll be dealing with all of the data, not just a sample (e.g., “I think I’ll find that Country A increased in life expectancy more than Country B did from year X to year Y”).
    • Is this hypothesis falsifiable, or, at least theoretically possible to prove wrong?
  • A statistical hypothesis – use this form if you’ll be working with data collected from a random sample taken from a population, and then using that sample data to draw conclusions about a larger population, such as with a survey, poll, or trial of some sort. Don’t forget, you’ll need a null hypothesis and an alternative hypothesis.

Quotes

“The only relevant test of the validity of a hypothesis is comparison of prediction with experience.”

Milton Friedman

“We see what we want to see, and observation conforms to hypothesis.“

Bergan Evans

“There are two possible outcomes: if the result confirms the hypothesis, then you’ve made a measurement. If the result is contrary to the hypothesis, then you’ve made a discovery.“

Enrico Fermi, Italian physicist

“I have steadily endeavoured to keep my mind free so as to give up any hypothesis, however much beloved (and I cannot resist forming one on every subject), as soon as facts are shown to be opposed to it.“

Charles Darwin

“In so far as a scientific statement speaks about reality, it must be falsifiable: and in so far as it is not falsifiable, it does not speak about reality.”

Sir Karl Popper, The Logic of Scientific Discovery

Further Learning

Previous Topic
Back to Lesson
Next Topic