1.2 A Review of Data Scale Types

Topic Summary

In Lesson 1 Topic 2, we will reintroduce the four different data scale types (nominal, ordinal, interval and ratio) proposed by Stanley Smith Stevens, a Harvard psychologist and researcher in 1946. These were reviewed in Data Literacy Fundamentals, but given their significance, we will briefly review them again here. The four scale types can be further grouped into categorical (nominal, ordinal) and quantitative (interval, ratio).  

Key Points to Remember

1. Nominal and ordinal scales are considered categorical because they define discrete levels of a variable that don’t have a consistent quantitative difference between them.
2. Interval and ratio are considered quantitative because they are measured and are conveyed by numbers whose intervals (gaps) are consistent.
3. The difference between categorical and quantitative scales will become critical as we consider how these variables can map to visual traits such as length, size and color.

Definitions

• nominal – a discrete classification of data, in which data are neither measured nor ordered but subjects are merely allocated to distinct categories: for example, a record of students’ course choices constitutes nominal data which could be correlated with school results. (source: dictionary.com)
• ordinal – a scale on which data is shown simply in order of magnitude since there is no standard of measurement of differences: for instance, a squash ladder is an ordinal scale since one can say only that one person is better than another, but not by how much. (source: dictionary.com)
• interval – a scale of measurement of data according to which the differences between values can be quantified in absolute but not relative terms and for which any zero is merely arbitrary: for instance, dates are measured on an interval scale since differences can be measured in years, but no sense can be given to a ratio of times. (source: dictionary.com)
• ratio – a scale of measurement of data which permits the comparison of differences of values; a scale having a fixed zero value. The distances travelled by a projectile, for instance, are measured on a ratio scale since it makes sense to talk of one projectile traveling twice as far as another. (source: dictionary.com)
• categorical – a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or nominal category on the basis of some qualitative property. (source: Wikipedia)
• quantitative – Numerical values with magnitudes that can be placed in a meaningful order with consistent intervals, also known as numerical. (source: Penn State)

Diagrams

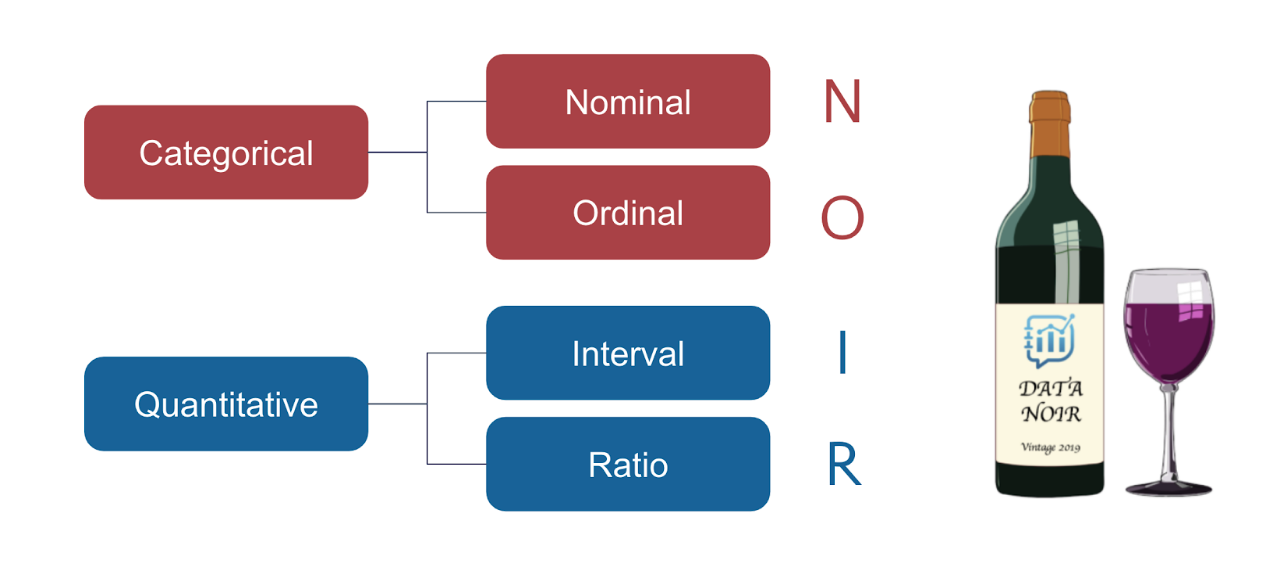
Since the four scale types formed the acronym N-O-I-R, we chose to remember them as a bottle of pinot noir – a type of red wine

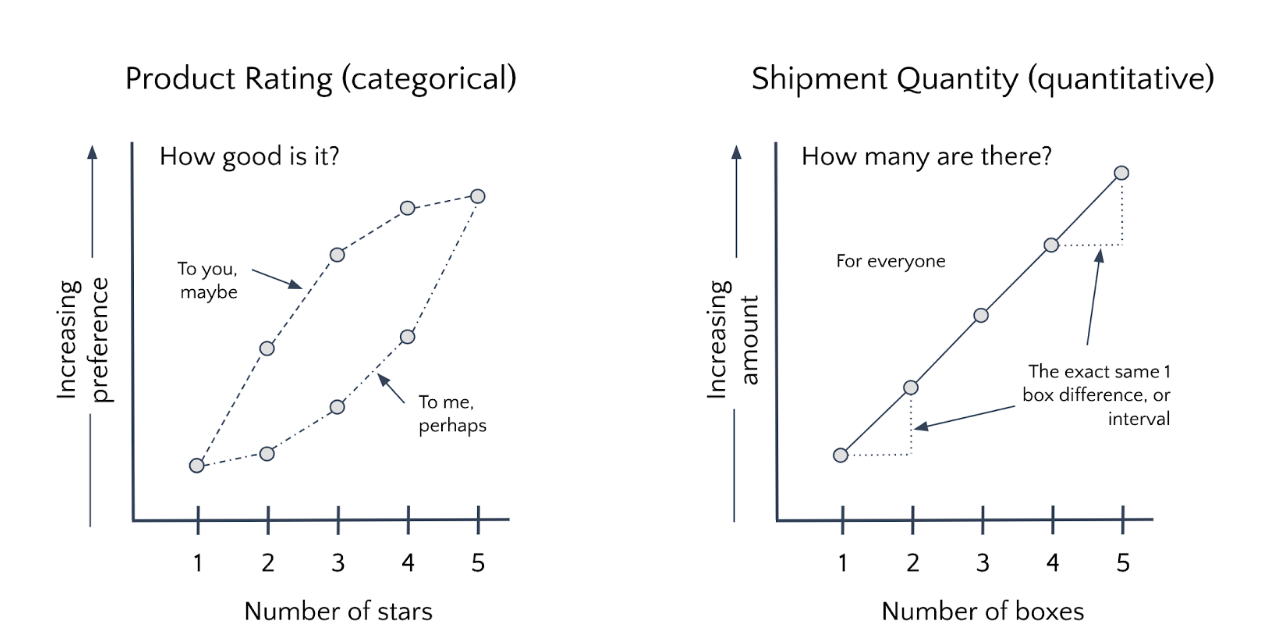
Quantitative scales preserve equality of intervals

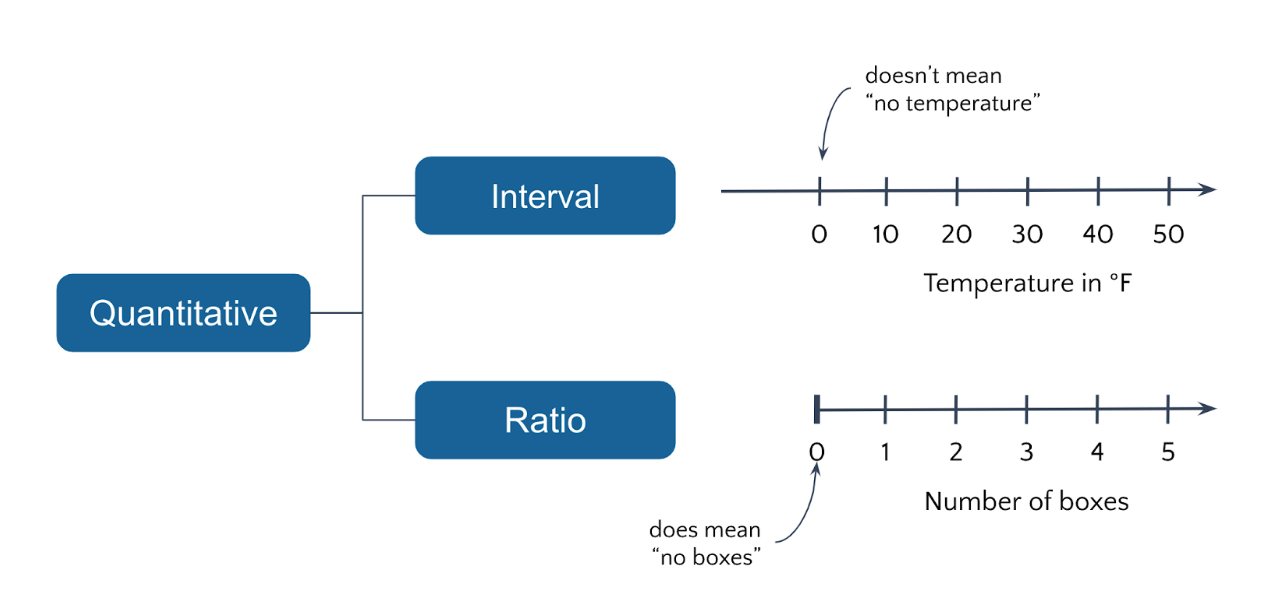
Presence of a “true” or “absolute” zero is the difference between ratio & interval

Exercises

Exercise 1.2. Data can be collected about any situation, object, or activity. Take a look at the photograph below and identify at least one variable of each scale type in the scene:

Quotes

“Perhaps agreement can better be achieved if we recognize that measurement exists in a variety of forms and that scales of measurement fall into certain definite classes. These classes are determined both by the empirical operations invoked in the process of “measuring” and by the formal (mathematical) properties of the scales. Furthermore – and this is of great concern to several of the sciences – the statistical manipulations that can legitimately be applied to empirical data depend upon the type of scale against which the data are ordered.”

Stanley Smith Stevens, from “On the Theory of Scales of Measurement“

Further Learning

• Video: Data Literacy Whiteboard #001 – The Four Data Scale Types