Do These 3 Classic Data Paradoxes
Fool You?
A Review of the Book “Innumeracy” by John Allen Paulos
“Innumeracy: Mathematical Illiteracy and Its Consequences” by John Allen Paulos was first published in 1988, but its argument and anecdotes have stood the test of time.
First off, what is innumeracy? Simply speaking, it’s the lack of ability to understand and use numbers in calculations. Whereas illiteracy is lack of competence with written words, innumeracy is lack of competence with numbers. And it’s not just for the uneducated. Even the well-educated struggle with numbers. Numeracy, the opposite of innumeracy, is one piece of the foundation upon which data literacy builds. You can’t have the latter without the former.
Consider this quote provided by Alberto Cairo, who’s on our board of advisors, for our course and companion book “The 17 Key Traits of Data Literacy.”

In “Innumeracy: Mathematical Illiteracy and Its Consequences,” John Allen Paulos argues that “our inability to deal rationally with very large numbers and the probabilities associated with them results in misinformed governmental policies, confused personal decisions, and an increased susceptibility to pseudoscience of all kinds. Innumeracy lets us know what we’re missing, and how we can do something about it.”
John Allen Paulos supports this argument with anecdotes from many aspects of modern life, and we wanted to share a few that we found most interesting. Read below or watch this video:
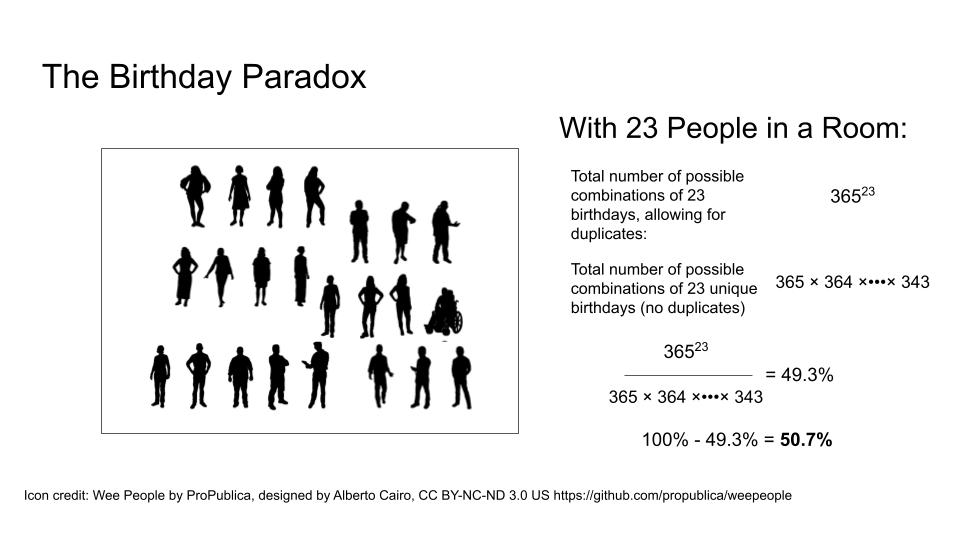
Paradox #1: The Birthday Paradox
You need 366 people in a room in order to be 100% certain that at least two of them share the same birthday (367 if you count leap year). But you only need 23 people in a room in order to have more than a 50% chance that at least two of them share the same birthday. People are often surprised by this. You think it’d be more right?
How do you calculate that? Well, with just three people in the room, there are already over 48.63 million possible combinations of birthdays if we allow for duplicates. Of those 48.63 million, 48.23 are unique (e.g., no two people share the same birthday). That means, there’s about a 99.18% chance no two people share the same birthday. Take the opposite (100% minus 99.18%), and you get 0.82% – the probability that at least two people share the same birthday in that group of three. Take the same math and adjust it to account for 23 people in the room, and that probability finally rises over 50%. It’s not rocket science, but it does require numeracy.
Paradox #2: Averaging Averages
How could a baseball player with a lower batting average in both the first and second half of a season, compared to another player, end up with a higher overall batting average at the end of the season?
In the book, John uses the example of two famous Yankee baseball players from the 20th century – Babe Ruth and Lou Gehrig. In a thought-experiment, let’s say that Babe Ruth has a better batting average than Lou Gehrig in both the first and second half of a season. Now, is it possible that Lou Gehrig actually ends up having the higher batting average overall? That seems impossible, right? But it turns out that it’s possible.
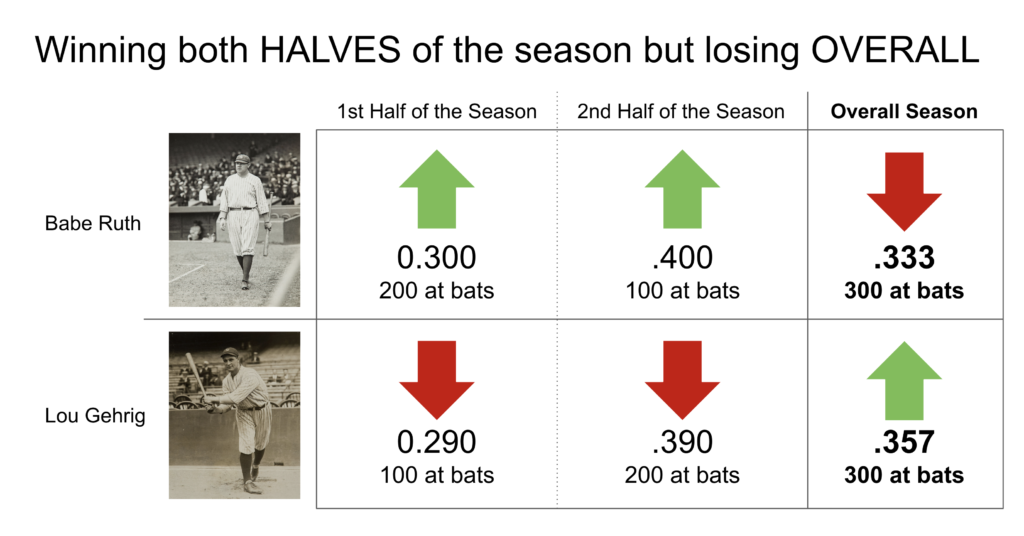
So what happened? The answer lies in the number of “at bats.” In the first half of the season Babe Ruth came to the plate twice as often as Lou Gehrig. The opposite happened in the second half of the season where both had a higher average, but Lou Gehrig had twice as many “at bats” than Babe Ruth. Thus, out of their equal number of 300 at bats, a higher percentage of Lou Gehrig’s were at that higher batting average level.
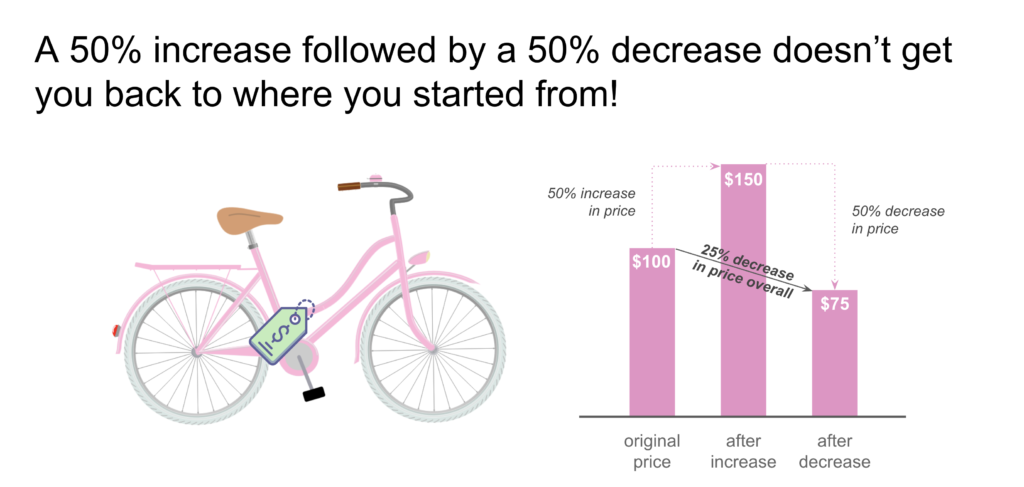
Paradox #3: Successive Percent Changes
The third and final cognitive trap we’d like to share from the book is related to percent change. Consider this scenario: You’ve got your eyes on buying a bicycle that costs $100. The retailer decides to increase the price by 50% to $150, so you decide to wait. They then decrease the price by 50%. How much does the bicycle cost now and by what percentage has the price decreased since its original price point of $100?
Intuitively, you might think that a 50% increase followed by a 50% decrease would get you back to where you started from, but it doesn’t because the new 50% decrease is being taken on top of that larger number ($150). The new price is $75 (50% of $150) and the overall price decreased by 25% ($100 minus $75 equals $25, which is 25% of $100).
A lot has changed since 1988. As the technological revolution speeds along, we have more tools and information than ever, but has reliance on these tools eroded our sixth sense and understanding of basic numerical concepts even further? Has humankind done itself a disservice by not placing enough importance on building the basic knowledge and skills to make good use of all these technological splendors? Before you google “How ChatGPT actually works,” it would be fruitful to take a step back to 1988 and invest time in grasping some very basic numerical concepts.






